使用动态规划算法实现两个文本的比对

动态规划算法是一种通过将问题拆分为子问题，并将子问题的解保存起来以避免重复计算的方法。动态规划算法的核心思想是利用已解决的子问题的解来求解当前问题，从而避免重复计算，提高求解效率。它在各个领域的问题求解中发挥着重要的作用，为解决复杂问题提供了强大的工具和方法。无论是在计算机科学、运筹学还是其他领域，动态规划算法都是解决问题的高效利器，值得深入学习和应用。

我们先以典型的斐波那契数列为例，简单介绍一下动态规划算法在解决问题中的应用过程。

斐波那契数列是一个以0和1开始，后续每一项都是前两项之和的数列。其数学表达式为：F(0) = 0，F(1) = 1，F(n) = F(n-1) + F(n-2)，其中n ≥ 2。

计算斐波那契数列，最简单的实现方式为递归：

public int fibonacci(int n) {
	if (n <= 1) {
		return n;
	} 
	return fibonacci(n - 1) + fibonacci(n - 2);
}

递归方式代码简洁，但是在计算较大的数列时会有性能问题，因为它会重复计算相同的子问题。比如说n = 4时，递归调用链如下图所示：

可以看到子问题f(2)存在重复计算，当n取值很大时，重复计算的子问题会更多，所以使用递归方式求解的效率十分低下。

使用动态规划算法可以高效地计算斐波那契数列，避免了重复计算，提高了计算效率。动态规划算法在计算斐波那契数列中的应用过程：

定义子问题：计算第n个斐波那契数F(n)，可以由子问题F(n-1)和F(n-2)得到。
确定状态转移方程：根据斐波那契数列的定义，我们可以得到状态转移方程

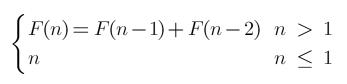定义好子问题和状态转移方程后，我们就可以使用动态规划算法来计算斐波那契数列（不考虑数值越界问题）：

public static int fibonacci(int n) {
	if (n <= 1) {
		return n;
	} 
    // dp[i]表示第i个斐波那契数的值
	int[] dp = new int[n+1];
    // 初始化边界值
    dp[0] = 0;
    dp[1] = 1;
	for (int i = 2; i < n; i++) {
        // f(n) = f(n-1) + f(n-2)
		dp[i] = dp[i-1] + dp[i-2];
	}
	return dp[n];
}

由于 F(n)只和 F(n−1)与 F(n−2)有关，因此可以使用「滚动数组思想」把空间复杂度优化成 O(1)：

public static int fibonacci(int n) {
	if (n <= 1) {
		return n;
	} 
	int prev = 0;
	int current = 1;
	for (int i = 2; i <= n; i++) {
		int temp = current;
		current = prev + current;
		prev = temp;
	}
	return current;
}

了解动态规划的基本原理后，我们开始探讨本次的主题：比对两个文本的差异。

在信息爆炸的时代，我们经常需要处理大量的文本数据。有时候，我们需要比对两个文本，找出它们之间的差异和相似之处。市面上有很多文本比对的工具，如Diff工具就可以快速识别出左右两边文本的差异并标识出来。

假设我们有两个文本：文本1和文本2，要比对它们之间的差异内容。

1.定义子问题：如果我们已知两个文本之间的最大公共序列的长度，在两个文本后面同时添加1个相同字符，则公共序列的长度在原本长度上加1。同时添加1个不相同字符，那么可能有以下三种情况：

原文本1最后一个字符与原文本2最后一个字符相同，公共序列的长度不变
原文本1最后一个字符与原文本2最后一个字符不同，但与新加的字符相同，公共子序列的长度加1
原文本1最后一个字符与原文本2最后一个字符不同，与新加的字符也不相同，公共序列的长度不变

我们可以定义dp[i][j]表示文本1前i个字符和文本2前j个字符之间公共子序列的最大长度。

2.确定状态转移方程：dp[i][j]的结果可以由三个子问题dp[i-1][j-1]、dp[i][j-1]、dp[i-1][j]推导出来

文本1的第i个字符等于文本2的第j个字符，dp[i][j] = dp[i-1][j-1] + 1
文本1的第i个字符不等于文本2的第j个字符, dp[i][j] = max(dp[i-1][j],dp[i][j-1])

得到状态转移方程：

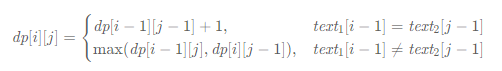3.边界值情况：当文本1和文本2其中一个字符数量为0时，显示公共子序列的长度为0，所以dp[i[0] = dp[0][j] = 0。

根据上述分析内容写出对应代码：

public int longestCommonSubsequence(String text1, String text2) {
	int m = text1.length(), n = text2.length();
	int[][] dp = new int[m + 1][n + 1];
	for (int i = 1; i <= m; i++) {
		char c1 = text1.charAt(i - 1);
		for (int j = 1; j <= n; j++) {
			char c2 = text2.charAt(j - 1);
			if (c1 == c2) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			} else {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}
	return dp[m][n];
}

当然，以上实现方式只是求出了公共子序列的最大长度，要得到具体的公共子序列，还需要通过回溯的方式，根据dp数组构造出最长公共子序列：

public String longestCommonSubsequence(String text1, String text2) {
	int m = text1.length(), n = text2.length();
	int[][] dp = new int[m + 1][n + 1];
	for (int i = 1; i <= m; i++) {
		char c1 = text1.charAt(i - 1);
		for (int j = 1; j <= n; j++) {
			char c2 = text2.charAt(j - 1);
			if (c1 == c2) {
				dp[i][j] = dp[i - 1][j - 1] + 1;
			} else {
				dp[i][j] = Math.max(dp[i - 1][j], dp[i][j - 1]);
			}
		}
	}

	// 回溯构造最长公共子序列
	StringBuilder builder = new StringBuilder();
	int i = m;
	int j = n;
	while (i > 0 && j > 0) {
		if (text1.charAt(i - 1) == text2.charAt(j - 1)) {
			builder.append(text1.charAt(i - 1));
			i--;
			j--;
		} else if (dp[i - 1][j] > dp[i][j - 1]) {
			i--;
		} else {
			j--;
		}
	}

	builder.reverse();

	return builder.toString();
}

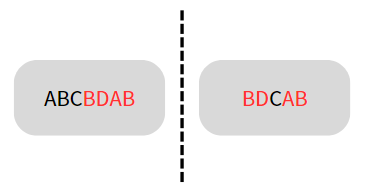
得到最长公共子序列后，我们就可以在原字符串上将公告序列标识出来，以字符串"ABCBDAB"和字符串"BDCAB"为例：

1.由上述代码得到公共序列为："BDAB"

2.标识公共序列

以上代码是一个简单的示例，仅用于说明动态规划算法求解最长公共子序列的基本思路。在实际应用中，可能需要考虑更多的边界情况和优化策略。